[3321]ヴィトゲンシュタインの『論理哲学論考』の謎を解く(1)
新年あけましておねでとうござます。今年もよろしくおねがいします。
さて、少々昔であるが、副島先生が「今日のぼやき」の中でルードビッヒ・ヴィトゲンシュタイン(1889- 1951)について書いている。ルードビッヒ・ヴィトゲンシュタインとはウィーン生まれの20世紀最大の哲学者である。哲学の問題すべてを一挙に解決したともいわれている。

ルートヴィヒ・ウィトゲンシュタイン(1889~1951)
私は前からヴィトゲンシュタインに興味をもっていたが、このぼやきの文章を読んでなるほどなあということがいくつかあった。ここでは、ヴィトゲンシュタインが用いた用語の解説をし、ヴィトゲンシュタインの『論理哲学論考』がなぜ重要なのかを、副島先生のぼやきの文章を補完する形で説明しようと思う。
というのは、既存の『論理哲学論考』の解説書では、どの哲学問題を、どう解決したのかという点について、なにも説明していないからだ。ある解説書の表紙には「哲学の問題すべてを一挙に解決するという野心的な試み」と書いてありながら、中ではこれについて言及していない。したがってヴィトゲンシュタインが何をやったのか、やろうとしたのかは、さっぱりわからない。
ちなみに、副島先生のぼやきでは、「精神と物体の二元論の問題について」解決したことがわかる。ここでは、別のことについてふれる。
さて、ヴィトゲンシュタインは『論理哲学論考』という本の中で、命題(proposition)、表現(representation)、射影(projection)、演算(operation)ということばを用いている。これらのことばは、実は数学用語である。特に表現(representation)は、数学で用いられる特殊な用語である。ヴィトゲンシュタインの『論理哲学論考』はなかなか理解されていないが、それは数学との類似性を使わないとうまく説明できないからだ。
表現(representation)というのは、表現論(representation theory)という形で数学の理論で用いられる。表現論は空間の線型変換を研究する数学の一分野である。例えば、高校の数学の範囲で言えば、三次元空間の平面や形を、別の空間に写像する場合が一番簡単な表現(representation)である。
ヴィトゲンシュタインは、この数学の「表現」を用いて、言語と事実で構成された「論理空間」を構築しようとしたが、実はそれは線型写像の行列による表現と非常に似通ったものである。
今、三次元の空間を行列で変換する場合を考えよう。式で表すと次のようになる。
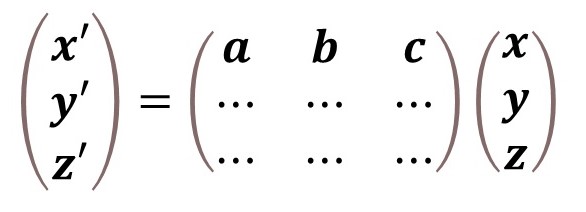
3つの括弧がある。実は、この真ん中の3行3列の行列が「表現」である。
そして、この式をじっくりと眺めてほしい。今、右のx、y、zというのは普通は座標である。3つしか入っていないが、実際は、空間でなくてもいいので、拡張していくらでも大きくすることができる。また、右と左の括弧には、座標以外の何が入ってもいい。ベクトルが入る場合を「ベクトル空間」、関数が入る場合を「ヒルベルト空間」という。
ヴィトゲンシュタインはこの右の括弧に事実(facts)を入れ、「論理空間」と名付けた。つまり、右の括弧に事実(fact)を入れた。これをatomic facts、つまり「原子のように無数にある、これ以上分解できない事実のかたまり」という。人間は生まれてから死ぬまで様々な経験をする。そのひとつひとつを拾い集めた経験的事実がこのatomic factsである。
このatomic factsを先ほどの行列という「表現」をつかって左側に変換する。
左側には1つの命題(proposition)がくる。図にすると下のようになる。

命題が「赤」とか「高い」とか、単純な単語である簡単な場合を考えてみよう。小さいころから我々は様々な赤いものを見てきている。赤い旗、赤い血、赤で塗られた皿・・・・・・。これらが原子的な事実である。そしてそこから、「赤」ということばが命題として構成される。「赤」という概念を抜き出しているわけだ。つまり、経験的事実から、「赤」ということばを抽出しているわけである。
このことをヴィトゲンシュタインは「射影」(projection)と名付けた。三次元のベクトル空間なら、球を平面に押し付けてつぶして二次元上で円にすること、一次元上で線分にすることを「射影」という。この性質の類似性をつかって、多数の事実(fact)から、「赤」という一次元のことばを「射影」しているわけだ。これがヴィトゲンシュタインのアイデアである。
ここまでは数学がわかっている人ならばなんとなくわかってもらえるだろう。問題はなぜこんなややこしいことを考えなければならないかということである。
それは、数学で、きちんと射影できない場合、「潰れている」と表すからである。逆にきちんと射影できた場合faithful(忠実)であるという。
この類似を使って、ヴィトゲンシュタインは諸事実からきちんと「射影」できた場合、その命題文は真(true)であるとした。逆に「射影」できない場合、それは偽(false)であるとした。
つまり、この方法で真偽が判定できる。
ただのことば遊びに見えるかもしれない。しかし、科学はこれと同じ仕組みで出てきている。例えばF(力)=m(質量)×a(加速度)という命題を考える。この物理の命題は様々な実験的な事実(experiments)や経験的事実(experience)から抽出して得られた式である。物が落下する、物体を動かすなどの多くの実験的事実から、この式(命題)が得られるわけだ。ヴィトゲンシュタインはこれを抽出ではなく「射影」という数学用語で表した。
つまり、事実からきちんと導出される命題のみが真である。様々な実験事実から理論を導く。このとき、諸事実からきちんと射影できれば、その命題は真である。逆に矛盾があれば偽(false)となる。例えば「風が吹けば桶屋が儲かる」という格言がある。それ格言自体は論理的におかしくない。ではそれが真かというと、その事実がない。だから、これは、論理的に正しくても真とはならない。
簡単にいえば、ヴィトゲンシュタインはこの数学の表現(representation)をつかって、「真と偽はどうやってきまるのか=論理とは何か」についての答えを導いたことになる。
ヴィトゲンシュタインはラッセルとフレーゲが「論理とは何か」に悩んでいるときに、数学に興味を持ち、ラッセルの追っかけみたいなことをやっていた。困ったラッセルにヴィトゲンシュタインは「私をきちがいだと思うか?」とラッセルに尋ねた。その時、ラッセルは「わからない、何か文章を書いて見せてくれ」といった。その時に書いた文章がこの「論理とは何か」についてだといわれている。
さて、この「諸事実が射影されている(反映されている)命題だけが真である」というのは、様々な諸学問を否定している。だからものすごく重要な概念である。
特に、数学にとってこれが意味することは非常に重要だ。数学では1 1=2になる。1 1=2となるのはそう決めた(公理)からではなく、ひとつのリンゴとひとつのリンゴをあわせるとふたつのリンゴになるという事実から発生していることを意味する。この考え方からすると「無限」「4次元空間」などはみんなあやしいものとなってしまう。諸事実が反映していない(射影されていない)命題は偽となってしまうからだ。
ただし、真の命題から別の命題を導くことは可能である。ウィトゲンシュタインはそのために、どのような場合にこれが成立するかもきちんと議論した。事実からえられる命題を基本的命題とか要素命題(elementary proposition)という。基本的命題を発展させれば別の命題を証明することができる。例えばF(力)=m(質量)×a(加速度)から、衛星は恒星のまわりを回転しているという別の命題が導ける。
しかし、それでも決まらない場合がある。つまり事実から「真」と「偽」が決まらない場合がある。これは、「真」か「偽」を決めるための事実がなにもない場合だ。「神が存在する」「無限は存在する」などがこれにあたる。
この場合は、「沈黙しなければならない」。これがウイトゲンシュタインが『論理哲学論考』の最後に述べたことば、「語りえぬものについては、沈黙しなければならない」の意味である。すべてここに帰着できる。
そして、これによって哲学が扱える範囲と境界が明確にできたわけだ。
つまり、ヴィトゲンシュタインはこのように哲学の成立する範囲と境界を決めることに成功した。このことを、「ボトルの中にいるハエを外に出して飛ぶようにする(To show the fly out of the fly bottle)」と表現する。ハエ(fly)は飛ぶ(fly)からハエ(fly)である。哲学も知識を愛するのだから、わからないことを議論していては哲学にならない。
以下続く
