最先端技術を直観的に理解する（２）　－　AIを理解するために必要な２つのことばは「機械学習」と「特徴表現」である

さて、ここでは私が昔書いた本、『物理学者が解き明かす思考の整理法』で記述した将棋のAI導入の方法を詳細に説明する。それによってAIとは何かが理解できる。

なぜ、将棋を扱うかというと、将棋のAIだけが、どのような数学的な技法をつかっているかが、よく理解できるからである。その他のAI、例えば画像解析もchatGPTもディープラーニングという方法を使っている。そのため、そのパラメーターが何をあらわしているのかが専門家でもわからない。もっと言えば、なぜよく解析できるかもわかっていない。したがって、その仕組みの説明を聞いても、しろうとには、さっぱりわからない。

そこで将棋である。

将棋はおよそ10の220乗の変化があるから、数十手すすむと、もう今までに指したことない未知の手が当然でてくる。ということは通常のデーターベースによるコンピュータープログラムでは、新しい局面がでてきて対処できない。

そこでゲームとして将棋をプログラミングする場合、次のようにプログラミングする。

①ある局面とその数手後までを数値化する。

②ある系統の中で最低値が最大になる系統をえらび次の手を選択する。

これを、ミニマックス探索、そして、ある系統の中で最低値を「ミニマックス探索値」とよぶ。つまり、相手がベストの手を指すと予測して、その中で一番いい手を選ぶようになっている。

だから将棋ソフトをつかっていると点数や勝利の確率が表示されるが、あれは、その時次にベストの手を指すと仮定した値が必ず表示されている。だから、いい手を指したとしても数値はよくならないし、悪手を指したときだけ相手の評価があがる。そういう仕組みになっている。

さて、上記の「①ある局面とその数手後までを数値化する」というのをもっと詳しく見てみよう。

この数値化の方法にはいろいろある。いちばん簡単な方法は、持ち駒の種類と数とか、自分の２つの駒の配置とかである。これを数値化してすべて足す。相手より点が多ければ、その差の点数だけ有利ということになる。

この数値化したものを「局面評価関数」という。これはどのゲームでも同じで、例えば、オセロという表裏が白黒の駒をひっくり返して、コマ数を争うゲームがある。このオセロでは、主に、同じ色の直線ができると高い局面評価関数が得られるようになっている。

将棋では、上に書いたように駒の配置と持ち駒が局面評価関数の指標となる。

この指標こそがAIで「特徴表現」と呼ばれるものである。

つまり、表現（representative　＝　代表）とは、ゲーム中の優勢劣勢を決めるために、数値化して代表した様々のパラメーターに他ならない。この指標の呼び方は、特徴表現だけでなく、評価パラメーター、特徴ベクトル、特徴量などいろいろある。ベクトルはその指標の数を次元として表せる。だから、十個の指標があれば「十次元のベクトル」として数学的にあらわされるのでベクトルと呼んでいるようだ。

この「特徴表現」は、持ち駒の種類とか、持っている２つの駒の配置とか、飛車や香車がどれほど動けるかなどの状況を得点としたものである。わかりやすく、例をあげておく。次図に示したのは、玉と金との関係で、王が８八（上）と９九（下）にある時の金の位置に対する得点つまり特徴表現である。見てわかるとおり、王に近いところに金がある、つまり守りが固いほど得点が高いということがわかる。

将棋が得意な人にはよくわかる図である。

さて、具体的に見てみる。今、図で王が８八にあるときに、金が６八から７八に移動したとする。すると、特徴表現のパラメーター値（特徴表現の数値）は－１６から３０に変化する。当然、他の特徴表現（金と銀の関係など）のパラメーター値も変化するから、それも合算する。つまり、このような特徴表現のパラメーター値がたくさんあり、指手により変化したすべての特徴表現のパラメーター値を合計して、局面評価関数とする。他には次のようなものが特徴表現となっている。

「王，他の駒２つの位置」、「王，隣接した味方の駒、他の味方の駒３つの位置」、「隣接しあった駒２つの位置関係」、「竜馬飛角桂香の利き上にいる駒の種類」、「竜馬飛角香が動ける枡の数」、「ピンされている駒の種類，方向，王との距離」、「角と同じ色の枡にいる味方の歩の数」、「歩桂銀が前進できるか」、「竜飛香の前・後の歩」、「王の周囲25枡の利きの配置」となっている。

これをすべて数値化して単純に足して局面評価関数とする。相手も同様に足して多い方が点が高く有利であることをあらわす。

実は、ここまではAIとはまったく関係がない。ここからがAIの出番である。

つまり、ここで問題がひとつでてくる。先ほどの図のパラメーター値（特徴表現の値）をどうやって決めたらいいのだろうかという問題だ。適当に決めてもいいが、それでは将棋の強いソフトとはならない。

保木邦仁氏という人は、「機械学習」という方法を用いて、これらの得点を決めた。具体的には、プロ棋士の対局データ六万局をもとにこの得点を決定した。つまり、「六万局の棋譜の指手を参考にして、プロ棋士が選択した指手が最良となるように特徴表現のパラメーター値（先ほどの図（王と金の関係）の得点）を決めたのである。」

このように過去のデータを自動的に処理させ、プログラムの機能を向上させる方法を「機械学習」という。これが２つめのキータームの「機械学習」である。

さて、さらに実際の特徴表現の得点の決め方を見ていこう。

６万局のプロ棋士の将棋対局、一局百手として約６００万の指手がある。これについて先ほどの特徴表現を最適化してみよう。

下の将棋のある場面を見てほしい。

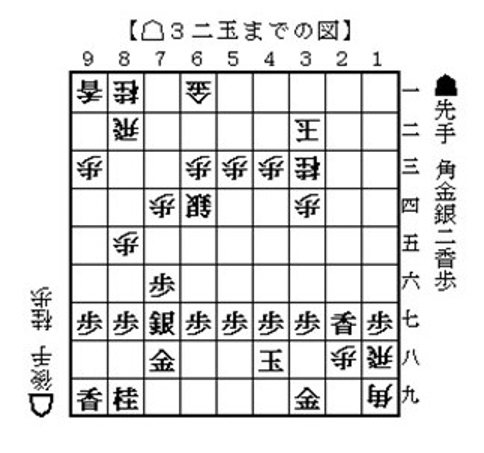
この局面でプロの指手が一手、　この局面でプロが指さなかった指手＝数十手があるとしよう。そして、この局面でプロの指手よりも大きな局面評価関数（＝ミニマックス探索値）を示した手の数を「目的関数」とする。つまりプロが指した手よりいい評価を示す指し手の数が評価関数である。通常プロがいちばんいい手を指すとすれば、０かあるいは１とか小さい値だろう。

これは上の局面だけであるが、同様に６００万手についてすべて同じことを行い、６００万手についてこれらをすべて足し合わせる。そしてそれを誤差関数とする。

今やりたいことは、プロ棋士が選択した指手が、他のどの指手よりも評価関数の値（ミニマックス探索値）が高くなるようにすることだ。これは、この誤差関数ができるだけ小さければいい。つまり、すべての特徴表現のパラメーター値をいじって変化させ、できるだけこの誤差関数を最低になるようにすればいい。

つまり、先ほどのすべての特徴表現のパラメーター値を少しずつ変化させ、この６００万の指手について足し合わせた誤差関数が最小になるように特徴表現のパラメーター値を決定するわけだ。これは最小勾配（こうばい）法と呼ばれている。

すると、「プロ棋士が選択した指手が最良となる」ということは、「６００万手について合計した誤差関数が最低値（停留値）をとるように特徴表現の得点を決定する」という数学命題に変わる。これなら、コンピューター計算でできる。

そして、一度、この特徴表現のパラメーター値が全部決定して完成してしまえば、それをつかって、まったく新しい将棋の局面でも、合計した値である局面評価関数値をミニマックス探索して、指手が決定できる。

現在ではプログラムの動作を決定づける１千万以上の特徴表現パラメーター値の最適化を行っていると書いてあるのを雑誌の記事で見たことがある。

まだ続きます。

下條竜夫拝